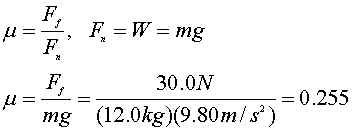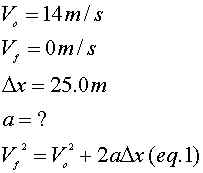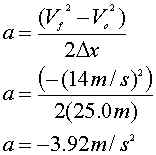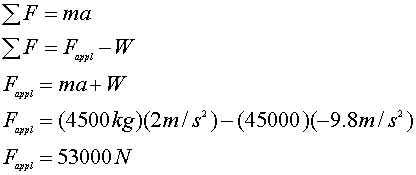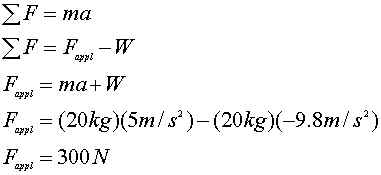Newton's Laws
Next Assignment (21-29)
11. A 95.0 kg
(209 lb) boxer has his first match in the Canal Zone (g = 9.782
m/s^2) and his second match at the North Pole (g = 9.832 m/s^2).
a. What is
his mass in the Canal Zone?
ans. 95kg
b. What is his weight in the
Canal Zone?
ans.

c. What is the mass at the
North Pole
ans. 95kg
d. What is his weight at the
North Pole?
ans.

e. Does he "weigh
in" or does he really "mass-in"?
ans.
Mass-in. Sometime the word mass is used to
replace the word weight.
12. Your new motorcycle weighs
2450 N. What is its mass in kilograms?
ans.
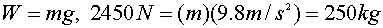
13. You place a 7.50kg
television set on a spring scale. If the scale reads 78.4N, what
is the acceleration of gravity at that location?
ans.

14. In Chapter 4 you calculated
the braking acceleration for a car based on data in a drivers'
handbook. The acceleration was -12.2 m/s^2.
If the car has a mass of 925kg, find the
frictional force and state the direction.
ans.
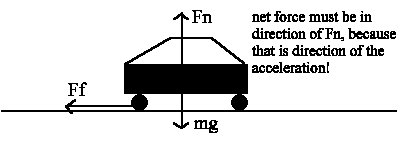
Since the only acceleration is in the
negative direction, the net force must be in that direction
(Newton's 2nd Law). The only force acting in that direction
is friction, so:
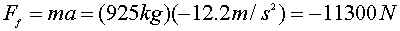
15. If you use a horizontal
force of 30.0N to slide a 12.0kg wooden crate across a floor at a
constant velocity, what is the coefficient of sliding friction
between crate and floor?
ans.
We have not talked about frictional force
yet, but you have enough knowledge to figure out how to
calculate it. There is a property that materials have called
coefficient of friction. The is represented by the Greek
letter mu "m". The force
caused by friction is:
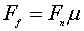
To solve this problem, all we need to do is
solve for m.

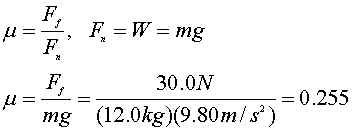
Notice that the coefficient of friction has
no units.
16. You are driving a 2500kg car
at a constant speed of 14.0 m/s along an icy, but straight and
level, road. While approaching a traffic light, it turns red. You
slam on the brakes. Your wheels lock, the tires begin skidding
and the car slides t a halt in a distance of 25.0m. What is the
coefficient of sliding friction (m) between
your tires and the icy roadbed?


now we have mg = a.
Now, since we do not know "a", we must use our
kinematic equations to find "a".
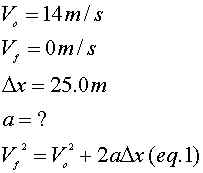
Solve equation 1 for "a" and PLUG and
CHUG!
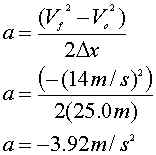
Now plug this value back into the relationship
that you found previously. (mg = a)

17. A person fishing hooks a 2.0
kg fish on a line that can only sustain a maximum of 38N of force
before breaking. At one point while reeling in the fish, it fights
back with a net force of 40N. What is the minimum acceleration
with which he must play out line during this time in order to
keep the line from breaking?
ans.


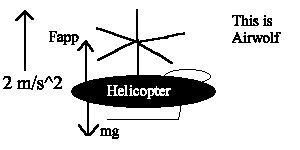
18. A 4500kg helicopter
accelerates upward at 2 m/s^2. What lift force is exerted by the
air on the propellers?
ans.
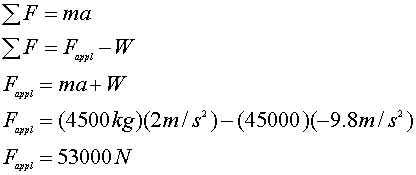
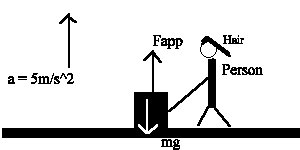
19. The maximum force a grocery
sack can withstand and not rip is 250N. If 20 kg of groceries are
lifted from the floor to a table with and acceleration of 5
m/s^2, will the sack hold?
ans.
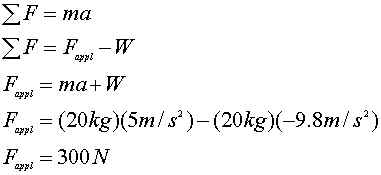
OPPS! the sack rips, because the
force is greater than 250N.
20. A student stands on a
bathroom scale in an elevator at rest on the 64th floor of a
building. The scale reads 836N.
a. As the elevator move up,
the scale reading increases to 935N, then decreases back to
836N. Find the acceleration of the elevator.
ans.


b. As the elevator
approaches the 74th floor, the scale reading drops as low as
782N. What is the acceleration of the elevator?
ans.

c. Using your results from
parts a and b, explain
which change in velocity, starting or stopping, would take
the longer time.
ans.
Stopping, because the acceleration is less
d. Explain the changes in
the scale you would expect on the ride back down.
ans.
As the elevator begins it decent
"a" is negative and the scale reads less than 836N.
When constant downward velocity is reached, the scale reads
836N since the acceleration in now zero. When the elevator is
slowing at the bottom, the acceleration is positive and the
scale reads more than 836N.
Next Assignment (21-29)
Home
![]()
![]()