Rolling a Ball down an incline!!
*NOTE: This problems requires a working knowledge of differential calculus.
I am going to start with a picture to set the problem up. I am just going to talk about the general case first, then move on to different conditions.
1. Now we want to add up all the forces in the "x" direction, and all the forces in the "y" direction.
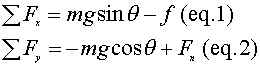
2. Now apply Newton's
2nd Law () to each
direction.
The displacement "Ycm" in the y direction is constant, because there is not acceleration in the Y direction so:
Substituting equation 5 into equation 4, we get:
3. Applying torque to the problem, we notice that the only force that is causing a torque is friction. Now if we can represent that frictional force in terms of the ball's rotational acceleration we can apply that to Newton's 2nd Law. Here is the way we are going to do it.
Torque is defined as Force times the lever arm, where f is the frictional force and r is the lever arm in this problem.
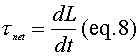
Torque is also define as the change in angular momentum. (equation 8)
Angular momentum is defined to be
L = Iw (eq.9)
where I = moment of Inertia and w is angular velocity.
Substituting eq. 7 into eq. 8, and eq. 8 into eq. 9 we get:
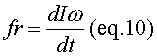
Since I is a property of the ball that does not change over time, we get
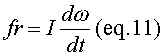
dw/dt = a where a is angular acceleration so:
fr = Ia (eq. 12)
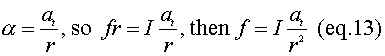
Now substitute eq.13 into eq. 1 and get
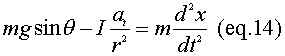
We no
that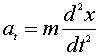 
, so we make
that substitution and solve for 
.
With the relationship obtained in equation 15, we have the ability to find the acceleration of ANY object rolling down an incline plane. This is the power of Calculus.
4. Since we know the
moment of inertia of a sphere to b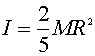e 
. We can find the acceleration of a ball
on and incline plane.
We will begin with equation 15 and substitute our value for moment of inertia and solve.
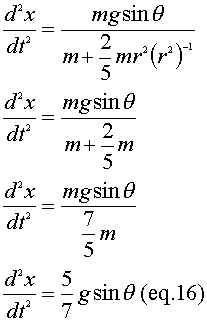
As you can see, the acceleration of the ball or any object is independent of the mass and the radius. This is REAL KEWL.
Back to Putt Physics
Now let us take the information we found in the previous problem and figure out how large we can make q before the ball begins to slide down the plane rather than rolling.
1. The first thing we must do is solve equation 13 for the frictional force.
substitute equation 16 into the above
Notice that we have solved for the frictional force, and it is independent of the coefficient of friction. NEAT!
2. Now since the ball is rolling, we can define the frictional force and substitute into equation 17 and see what we get.
now substitute equation 17 into 18 and solve.
What we have found is if the tan of q is larger than (7/2)ms, the ball is going to slip before it rolls.
Back to Putt Physics